הבדלים בין גרסאות בדף "88-617 תשעט סמסטר א"
(←תרגילי בית) |
|||
| (48 גרסאות ביניים של 3 משתמשים אינן מוצגות) | |||
| שורה 4: | שורה 4: | ||
מתרגל: אריאל ויצמן, relweiz@gmail.com. | מתרגל: אריאל ויצמן, relweiz@gmail.com. | ||
| + | |||
| + | =מבחן תשעט= | ||
| + | |||
| + | *[[מדיה:ExmMoedA_88617_79.pdf|מועד א']] | ||
| + | |||
| + | *[[מדיה:ExmMoedASol_88617_79.pdf|פתרון מועד א']] | ||
| + | |||
| + | *[[מדיה:ExmMoedB_88617_79.pdf|מועד ב']] | ||
| + | |||
| + | *[[מדיה:ExmMoedBSol_88617_79.pdf|פתרון מועד ב']] | ||
| + | |||
| + | ==המבחן== | ||
| + | |||
| + | מבנה המבחן: במבחן יהיו 6 שאלות, בלי בחירה, משקל כל שאלה 20 נקודות. | ||
| + | |||
| + | נושאים: | ||
| + | |||
| + | שאלה 1- 2 השיעורים הראשונים (חיבור, חיסור, כפל חילוק במספרים מרוכבים. צמוד, נורמה, חלק ממשי וחלק מדומה. העלה בחזקה והוצאת שורשים לפי נוסחת דה מואבר. מעבר בין הצגות: פולרית וקרטזית). | ||
| + | |||
| + | שאלה 2- חישוב של פונקציה מרוכבת מיוחדת (סינוס, קוסינוס, פונקציה מעריכית, לוגריתם וחזקות) | ||
| + | |||
| + | שאלה 3- הוכחת טענה על פונקציות מרוכבות מיוחדות. | ||
| + | |||
| + | שאלה 4- בדיקה האם פונקציה היא גזירה לפי משוואות קושי- רימן, וחישוב הנגזרת. | ||
| + | |||
| + | שאלות 5 ו6- פתירת מד"רים (מציאת פתרון כללי, או פתרון פרטי בהינתן תנאי התחלה). | ||
| + | |||
| + | *[[מדיה:ExmTest1_88617_79.pdf|מבחן לדוגמא]] | ||
| + | |||
| + | *[[מדיה:ExmTest1sol_88617_79.pdf|מבחן לדוגמא- פתרון]] | ||
| + | |||
| + | *[[מדיה:ExmTest2_88617_79.pdf|שאלות לאימון]] | ||
| + | |||
| + | *[[מדיה:ExmTest2sol_88617_79.pdf|שאלות לאימון- פתרונות]] | ||
| + | |||
| + | *[[מדיה:DafNuschot_88617_79.pdf|דף נוסחאות]]- לנוחיותכם, מצורף דף הנוסחאות שיהיה במבחן. | ||
| + | |||
| + | ==רשימת נושאים== | ||
| + | |||
| + | בפונקציות מרוכבות: | ||
| + | 1. מספרים מרוכבים: הגדרה, הצגה פולרית וקרטזית, נורמה וצמוד, פעולות חשבוניות. | ||
| + | |||
| + | 2. סדרות והתכנסות | ||
| + | |||
| + | 3. פונקציות רציפות וגזירות. | ||
| + | |||
| + | 4. משוואות קושי רימן. | ||
| + | |||
| + | 5. פונקציות טריגונומטריות מרוכבות. | ||
| + | |||
| + | 6. חזקות ולוגריתמים מרוכבים. | ||
| + | |||
| + | את כל החומר ניתן למצוא בספרי האוניברסיטה הפתוחה של הקורס "פונקציות מרוכבות", יחידות 1-3. | ||
| + | |||
| + | במשוואות דיפרנציאליות: | ||
| + | |||
| + | 1. משוואות לינאריות מסדר ראשון. | ||
| + | |||
| + | 2. משפט הקיום והיחידות למשוואות מסדר ראשון. | ||
| + | |||
| + | 3. משוואות פרידות. | ||
| + | |||
| + | 4. משוואות מדוייקות. | ||
| + | |||
| + | 5. גורם אינטגרציה. | ||
| + | |||
| + | 6. משוואות שנפתרות באמצעות הצבה. | ||
| + | |||
| + | 7. משוואות ברנולי. | ||
| + | |||
| + | 8. משוואות הומוגניות. | ||
| + | |||
| + | משוואות מסדר שני: | ||
| + | |||
| + | 9. הורדת סדר משוואה. | ||
| + | |||
| + | 10. מרחב הפתרונות של משוואה לינארית מסדר שני. | ||
| + | |||
| + | 11. משפט הקיום והיחידות למשוואה לינארית מסדר שני. | ||
| + | |||
| + | 12. וריאציית הפרמטרים. | ||
| + | |||
| + | 13. שיטת השוואת המקדמים. | ||
| + | |||
| + | 14. מערכת משוואות לינאריות עם מקדמים קבועים. | ||
| + | |||
| + | |||
==קישורים== | ==קישורים== | ||
| שורה 15: | שורה 102: | ||
תרגילי הבית שיועלו לכאן הינם ללא הגשה. | תרגילי הבית שיועלו לכאן הינם ללא הגשה. | ||
| − | *[[מדיה:Ex1_88617_79|תרגיל 1]] | + | *[[מדיה:Ex1_88617_79.pdf|תרגיל 1]]. יש טעות בשאלה 5, אז להלן השאלה החדשה: נניח שאנחנו מסמנים במישור המרוכב את כל המספרים <math>z</math> המקיימים <math>z+\overline{z}=8</math>. מה נקבל? [[מדיה:Ex1_88617_79Sol.pdf|פתרון תרגיל 1]]. בפתרון שאלה 4 הפכתי בטעות בתשובה הסופית בין החלק הממשי למדומה. |
| + | |||
| + | *[[מדיה:Ex2_88617_79.pdf|תרגיל 2]]. [[מדיה:Ex2_88617_79SolUp.pdf|פתרון תרגיל 2]]. | ||
| + | |||
| + | *[[מדיה:Ex3_88617_79.pdf|תרגיל 3]]. [[מדיה:Ex3_88617_79Sol.pdf|פתרון תרגיל 3]]. | ||
| + | |||
| + | *[[מדיה:Ex4_88617_79Updated.pdf|תרגיל 4]]. [[מדיה:Ex4_88617_79SolUpdated.pdf|פתרון תרגיל 4]]. | ||
| + | |||
| + | *[[מדיה:Ex5_88617_79.pdf|תרגיל 5]]. [[מדיה:Ex5_88617_79Sol.pdf|פתרון תרגיל 5]]. | ||
| + | |||
| + | *[[מדיה:Ex6_88617_79.pdf|תרגיל 6]]. [[מדיה:Ex6_88617_79SolUpdated2.pdf|פתרון תרגיל 6]]. הועלה פתרון מתוקן, סליחה על הטעויות. | ||
| + | |||
| + | *[[מדיה:Ex7_88617_79.pdf|תרגיל 7]]. [[מדיה:Ex7_88617_79SolUp.pdf|פתרון תרגיל 7]]. | ||
| + | |||
| + | תיקון טעות: בשאלה 1 סעיף ב, טעיתי כשעשיתי מכנה משותף... להלן הפתרון הנכון: | ||
| + | |||
| + | <math>(1+i)^{2i}=e^{2i\cdot L(\sqrt{2}cis(\frac{\pi}{4}+2\pi k)}=e^{2i\cdot (\ln \sqrt{2}+i(\frac{\pi}{4}+2\pi k))}=e^{-\frac{\pi}{2}+4\pi k+2\ln \sqrt{2}i}=e^{-\frac{\pi}{2}+4\pi k}cis(2\ln \sqrt{2})</math> | ||
| + | |||
| + | *[[מדיה:Ex8_88617_79.pdf|תרגיל 8]]. [[מדיה:Ex8_88617_79Sol.pdf|פתרון תרגיל 8]]. | ||
| + | |||
| + | בשאלה 1 סעיף ג יש טעות קטנה: השורשים הם <math>1\pm 3i</math>. | ||
| + | |||
| + | בשאלה 3 סעיף ג: במציאת הפתרון הפרטי יש טעות נגררת, לא הכפלתי את <math>2b</math> ב-<math>4</math>. | ||
| + | |||
| + | בנוסף, נכנסו לי בטעות שני סעיפים לא הומוגניים, אז להלן המשך הפתרון לסעיפים אלו: | ||
| + | |||
| + | ב. <math>2</math> איננו שורש, ולכן ננחש פתרון פרטי מהצורה <math>y=ae^{2x}</math>. ולכן: <math>y'=2ae^{2x},y''=4ae^{2x}</math>. נציב במד"ר: <math>36ae^{2x}+12ae^{2x}+ae^{2x}=e^{2x}</math> ולכן <math>49a=1</math> כלומר, <math>a=\frac{1}{49}</math>. קיבלנו <math>y_p=\frac{1}{49}e^{2x}</math>, ולכן הפתרון הכללי הוא: <math>y=C_1e^{-\frac{1}{3}x}+C_2xe^{-\frac{1}{3}x}+\frac{1}{49}e^{2x}</math>. | ||
| + | |||
| + | ה. ננחש פתרון פרטי ממעלת החלק הלא הומוגני: <math>y=bx+2,y'=b,y''=0</math>. נציב במד"ר: <math>10bx+10c=2x</math>, ומהשוואת מקדמים נקבל <math>b=\frac{1}{5},c=0</math> כלומר, <math>y_p=\frac{1}{5}x</math>. לכן פתרון כללי הוא: <math>y=C_1\cos \sqrt{10}x+C_2\sin \sqrt{10}x+\frac{1}{5}x</math>. | ||
גרסה אחרונה מ־10:14, 1 במרץ 2019
88-617 מבוא לאנליזה מתקדמת למורים
מרצה: תמר בר-און, tamarnachshoni@gmail.com.
מתרגל: אריאל ויצמן, relweiz@gmail.com.
תוכן עניינים
מבחן תשעט
המבחן
מבנה המבחן: במבחן יהיו 6 שאלות, בלי בחירה, משקל כל שאלה 20 נקודות.
נושאים:
שאלה 1- 2 השיעורים הראשונים (חיבור, חיסור, כפל חילוק במספרים מרוכבים. צמוד, נורמה, חלק ממשי וחלק מדומה. העלה בחזקה והוצאת שורשים לפי נוסחת דה מואבר. מעבר בין הצגות: פולרית וקרטזית).
שאלה 2- חישוב של פונקציה מרוכבת מיוחדת (סינוס, קוסינוס, פונקציה מעריכית, לוגריתם וחזקות)
שאלה 3- הוכחת טענה על פונקציות מרוכבות מיוחדות.
שאלה 4- בדיקה האם פונקציה היא גזירה לפי משוואות קושי- רימן, וחישוב הנגזרת.
שאלות 5 ו6- פתירת מד"רים (מציאת פתרון כללי, או פתרון פרטי בהינתן תנאי התחלה).
- דף נוסחאות- לנוחיותכם, מצורף דף הנוסחאות שיהיה במבחן.
רשימת נושאים
בפונקציות מרוכבות: 1. מספרים מרוכבים: הגדרה, הצגה פולרית וקרטזית, נורמה וצמוד, פעולות חשבוניות.
2. סדרות והתכנסות
3. פונקציות רציפות וגזירות.
4. משוואות קושי רימן.
5. פונקציות טריגונומטריות מרוכבות.
6. חזקות ולוגריתמים מרוכבים.
את כל החומר ניתן למצוא בספרי האוניברסיטה הפתוחה של הקורס "פונקציות מרוכבות", יחידות 1-3.
במשוואות דיפרנציאליות:
1. משוואות לינאריות מסדר ראשון.
2. משפט הקיום והיחידות למשוואות מסדר ראשון.
3. משוואות פרידות.
4. משוואות מדוייקות.
5. גורם אינטגרציה.
6. משוואות שנפתרות באמצעות הצבה.
7. משוואות ברנולי.
8. משוואות הומוגניות.
משוואות מסדר שני:
9. הורדת סדר משוואה.
10. מרחב הפתרונות של משוואה לינארית מסדר שני.
11. משפט הקיום והיחידות למשוואה לינארית מסדר שני.
12. וריאציית הפרמטרים.
13. שיטת השוואת המקדמים.
14. מערכת משוואות לינאריות עם מקדמים קבועים.
קישורים
מערכי תרגול באנליזה מתקדמת למורים
תרגילי בית
תרגילי הבית שיועלו לכאן הינם ללא הגשה.
- תרגיל 1. יש טעות בשאלה 5, אז להלן השאלה החדשה: נניח שאנחנו מסמנים במישור המרוכב את כל המספרים
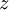 המקיימים
המקיימים 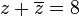 . מה נקבל? פתרון תרגיל 1. בפתרון שאלה 4 הפכתי בטעות בתשובה הסופית בין החלק הממשי למדומה.
. מה נקבל? פתרון תרגיל 1. בפתרון שאלה 4 הפכתי בטעות בתשובה הסופית בין החלק הממשי למדומה.
- תרגיל 6. פתרון תרגיל 6. הועלה פתרון מתוקן, סליחה על הטעויות.
תיקון טעות: בשאלה 1 סעיף ב, טעיתי כשעשיתי מכנה משותף... להלן הפתרון הנכון:
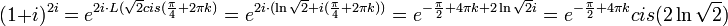
בשאלה 1 סעיף ג יש טעות קטנה: השורשים הם 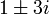 .
.
בשאלה 3 סעיף ג: במציאת הפתרון הפרטי יש טעות נגררת, לא הכפלתי את 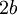 ב-
ב-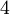 .
.
בנוסף, נכנסו לי בטעות שני סעיפים לא הומוגניים, אז להלן המשך הפתרון לסעיפים אלו:
ב. 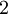 איננו שורש, ולכן ננחש פתרון פרטי מהצורה
איננו שורש, ולכן ננחש פתרון פרטי מהצורה 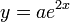 . ולכן:
. ולכן: 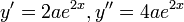 . נציב במד"ר:
. נציב במד"ר: 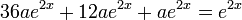 ולכן
ולכן 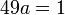 כלומר,
כלומר, 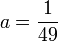 . קיבלנו
. קיבלנו 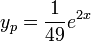 , ולכן הפתרון הכללי הוא:
, ולכן הפתרון הכללי הוא: 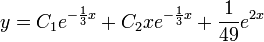 .
.
ה. ננחש פתרון פרטי ממעלת החלק הלא הומוגני: 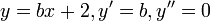 . נציב במד"ר:
. נציב במד"ר: 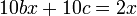 , ומהשוואת מקדמים נקבל
, ומהשוואת מקדמים נקבל 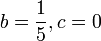 כלומר,
כלומר, 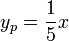 . לכן פתרון כללי הוא:
. לכן פתרון כללי הוא: 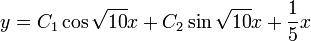 .
.