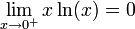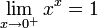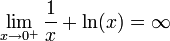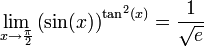חדוא 1 - ארז שיינר
מתוך Math-Wiki
גרסה מ־16:38, 19 בפברואר 2022 מאת יונתן871 (שיחה | תרומות) (←הצעות פתרון למבחנים מהשנים תשע"ה-תשפ"ב (תיכוניסטים))
אהבתם חדו"א 1? אז תעופו על חדו"א 2!
תוכן עניינים
- 1 תרגילי הכנה למבחן ופתרונותיהם
- 2 מבחנים ופתרונות
- 3 סרטוני ותקציר ההרצאות
- 3.1 פרק 1 - מספרים וחסמים
- 3.2 פרק 2 - סדרות
- 3.2.1 הגדרת הגבול
- 3.2.2 שאיפה לאפס
- 3.2.3 משפטי סנדביץ'
- 3.2.4 מבוא לחשבון גבולות (אריתמטיקה של גבולות)
- 3.2.5 אינדוקציה
- 3.2.6 חזקת אינסוף
- 3.2.7 כלל המנה
- 3.2.8 חזקות של גבולות
- 3.2.9 סדרות מונוטוניות והמספר e
- 3.2.10 תתי סדרות וגבולות חלקיים
- 3.2.11 כלל הe
- 3.2.12 חשבון גבולות (אריתמטיקה של גבולות)
- 3.2.13 קריטריון קושי לסדרות
- 3.3 פרק 3 - טורים
- 3.4 פרק 4 - פונקציות ורציפות
- 3.5 פרק 5 - גזירות
- 3.6 פרק 6 - חקירה
תרגילי הכנה למבחן ופתרונותיהם
מבחנים ופתרונות
מערכי תרגול עם פתרונות
מבחנים של מתמטיקה
- מבחן מועד א' החממה תשפ"א, פתרון
- מבחן מועד ב' החממה תשפ"א, פתרון
- פתרון מבחן לדוגמא החממה תשפ"א
- מבחן מועד א תשע"ט, פתרון
- מבחן דמה תשע"ז, פתרון
- מבחן מועד א' תשע"ז, פתרון
- מבחן מועד ב' תשע"ז, פתרון
- מבחן מועד א' תשע"ו, פתרון המרצה, פתרון המתרגלים, פתרון ארז שיינר
- מבחן מועד א' תשע"ג, פתרון
- מבחן מועד ב' תשע"ג, פתרון חלקי
- מבחן דמה למתמטיקאים תשע"ב, פתרון
- מבחן דמה נוסף תשע"ב, פתרון
- מועד מיוחד תשע"ב, פתרון
- מועד א' תשע"ב, פתרון
- מועד ב' למתמטיקאים תשע"ב כולל פתרון
- מבחן מועד א' החממה תשע"א פתרון
- מבחן מועד ב' החממה תשע"א פתרון
- פתרון תשס"ב, מועד א
- פתרון תשס"ג, מועד ב
- פתרון תשנ"ט, מועד ב
- פתרון תש"נ, אין מועד
- פתרון תשנ"ו, מועד ב'
מבחנים של מדמ"ח
- מועד א' סמסטר קיץ תשפ"א
- מועד ב' סמסטר קיץ תשפ"א
- מבחן לדוגמא תשפ"א, פתרון מבחן לדוגמא תשפ"א
- מועד א' תשפ"א, פתרון מועד א' תשפ"א
- מועד ב' תשפ"א, פתרון מועד ב' תשפ"א
- מועד ג' תשפ"א, פתרון מועד ג' תשפ"א
- מבחן לדוגמא תש"ף, פתרון מבחן לדוגמא תש"ף
- מבחן מועד א' תש"ף, פתרון מבחן מועד א' תש"ף
- פתרון מבחן מועד ג' תשע"ז
- מועד א' תשע"ג פתרונות בלבד
- מבחן דמה תשע"ג, פתרון מבחן דמה תשע"ג
- מבחן מדמ"ח מועד א' תשעב ופתרונו.
מבחנים של הנדסה
- מבחנים בחדו"א 1 של הנדסה - שאלות 2,6 אינן רלונטיות לקורס זה
מבחנים של אנליזה למורים
- מבחנים בקורס אנליזה 1 למורים - אמנם כלל השאלות רלוונטיות, אולם הרמה הכולל של המבחנים נמוכה יותר מקורס זה
הצעות פתרון למבחנים מהשנים תשע"ה-תשפ"ב (תיכוניסטים)
ע"י לירן מנצורי ויונתן סמידוברסקי
- מבחן תשע"ח מועד א'
- מבחן תשע"ז מועד ב'
- מבחן תשע"ז מועד א'
- מבחן תשע"ו מועד ב'
- מבחן תשע"ו מועד א'
- מבחן תשע"ה מועד ב'
- מבחן תשע"ה מועד א'
מבחנים מאוניברסיטאות שונות
סרטוני ותקציר ההרצאות
פלייליסט ההרצאות של אינפי 1 למדמח תשפ"א
פרק 1 - מספרים וחסמים
קבוצות מספרים
- הטבעיים
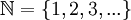
- השלמים
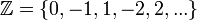
- הרציונאליים
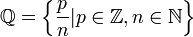
- הממשיים
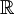 , כל השברים העשרוניים כולל האינסופיים
, כל השברים העשרוניים כולל האינסופיים
- העשרה: בנייה של שדה הממשיים באמצעות חתכי דדקינד
- לא קיים
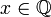 כך ש
כך ש 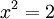 .
. - במילים פשוטות,
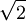 אינו רציונאלי (בהמשך נוכיח שיש מספר ממשי כזה).
אינו רציונאלי (בהמשך נוכיח שיש מספר ממשי כזה).
חזקות ולוגריתמים
- לכל מספר ממשי
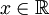 ולכל מספר טבעי
ולכל מספר טבעי 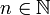 נגדיר
נגדיר 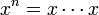 כפל n פעמים
כפל n פעמים - לכל מספר ממשי אי שלילי
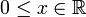 ולכל מספר טבעי
ולכל מספר טבעי 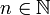 נגדיר
נגדיר ![x^{\frac{1}{n}}=\sqrt[n]{x}](/images/math/a/a/4/aa47c95f75d6ca9957b56ec9d60adad7.png) כלומר המספר האי שלילי שבחזקת n שווה לx.
כלומר המספר האי שלילי שבחזקת n שווה לx. - לכל מספר ממשי אי שלילי
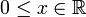 ולכל זוג מספרים טבעיים
ולכל זוג מספרים טבעיים 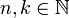 נגדיר
נגדיר ![x^{\frac{n}{k}}=\sqrt[k]{x^n}](/images/math/0/d/8/0d887c7e78d7d80ed9cdfc4a3456f04f.png)
- לכל מספר ממשי
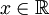 נגדיר
נגדיר 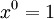
- מה לגבי חזקות ממשיות אי רציונליות?
- נגדיר אותן באמצעות גבול של חזקות רציונאליות
- לכל מספר ממשי
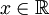 ולכל חזקה ממשית שלילית
ולכל חזקה ממשית שלילית 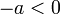 נגדיר
נגדיר 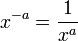
- לכל
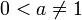 נגדיר את
נגדיר את 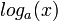 להיות המספר שa בחזקתו שווה לx.
להיות המספר שa בחזקתו שווה לx. - חוקי לוגים:
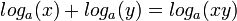
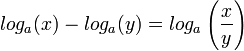
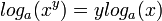
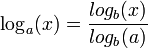
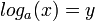 אם ורק אם
אם ורק אם 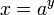
חסמים
- תהי
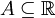 אזי:
אזי:
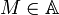 נקרא המקסימום של A או האיבר הגדול ביותר של A אם לכל
נקרא המקסימום של A או האיבר הגדול ביותר של A אם לכל  מתקיים כי
מתקיים כי 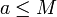
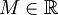 נקרא חסם מלעיל של A אם לכל
נקרא חסם מלעיל של A אם לכל  מתקיים כי
מתקיים כי 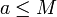
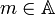 נקרא המינימום של A או האיבר הקטן ביותר של A אם לכל
נקרא המינימום של A או האיבר הקטן ביותר של A אם לכל  מתקיים כי
מתקיים כי 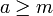
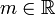 נקרא חסם מלרע של A אם לכל
נקרא חסם מלרע של A אם לכל  מתקיים כי
מתקיים כי 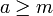
- כמו כן:
- אם יש איבר קטן ביותר בקבוצת חסמי המלעיל של A הוא נקרא החסם העליון של A, או הסופרמום של A ומסומן
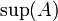
- אם יש איבר גדול ביותר בקבוצת חסמי המלרע של A הוא נקרא החסם התחתון של A, או האינפימום של A ומסומן
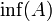
- אם יש איבר קטן ביותר בקבוצת חסמי המלעיל של A הוא נקרא החסם העליון של A, או הסופרמום של A ומסומן
- בשדה הממשיים לכל קבוצה לא ריקה וחסומה מלעיל יש חסם עליון, ולכל קבוצה לא ריקה וחסומה מלרע יש חסם תחתון.
- בשדה הרציונאליים זה לא נכון; לקבוצה
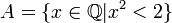 אין מספר רציונאלי קטן ביותר מבין חסמי המלעיל שלה.
אין מספר רציונאלי קטן ביותר מבין חסמי המלעיל שלה.
- תהי
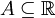 ויהי
ויהי 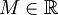 אזי:
אזי:
- M הוא החסם העליון של A אם ורק אם M הוא חסם מלעיל של A ולכל מספר
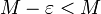 קיים מספר
קיים מספר  כך ש
כך ש 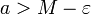
- m הוא החסם התחתון של A אם ורק אם m הוא חסם מלרע של A ולכל מספר
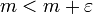 קיים מספר
קיים מספר  כך ש
כך ש 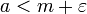
- M הוא החסם העליון של A אם ורק אם M הוא חסם מלעיל של A ולכל מספר
- דוגמא: תהיינה
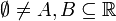 חסומות מלעיל כך שA אינה מכילה חסמי מלעיל של B, אזי
חסומות מלעיל כך שA אינה מכילה חסמי מלעיל של B, אזי 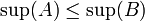
שיטות הוכחה בסיסיות
- הוכחת טענות מכומתות - טענות 'לכל' וטענות 'קיים'
פרק 2 - סדרות
הגדרת הגבול
- הגדרת הגבול של סדרה:
- תהי סדרה ממשית
 ויהי מספר ממשי
ויהי מספר ממשי 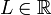 .
. 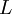 הינו גבול הסדרה
הינו גבול הסדרה  (מסומן
(מסומן 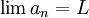 או
או 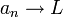 ) אם:
) אם:
- לכל סביבה של הגבול, קיים מקום בסדרה שאחריו כל איברי הסדרה נמצאים בסביבה הנתונה, כלומר:
- לכל מרחק
 קיים מקום
קיים מקום 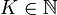 כך שאחריו לכל
כך שאחריו לכל 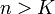 מתקיים כי
מתקיים כי 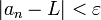
- נגדיר ש
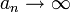 אם לכל
אם לכל 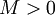 קיים
קיים 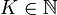 כך שלכל
כך שלכל 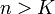 מתקיים כי
מתקיים כי 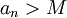
- נגדיר ש
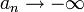 אם
אם 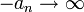
- טענה: תהי
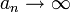 אזי
אזי 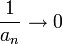
- טענה: תהי
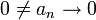 אזי
אזי 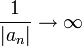
- אם
 וכן
וכן 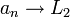 אזי
אזי 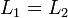
- סדרה המתכנסת לגבול סופי חסומה.
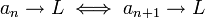
- בפרט, כל שינוי, תוספת או החסרה של מספר סופי של איברים לא משפיע על גבול הסדרה.
- תהי סדרה
 המתכנסת לגבול סופי והמקיימת לכל
המתכנסת לגבול סופי והמקיימת לכל  כי
כי 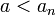 אזי
אזי 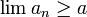
שאיפה לאפס
- תהי סדרה
 ויהי
ויהי 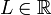 אזי
אזי 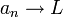 אם ורק אם
אם ורק אם 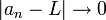
- בפרט
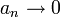 אם ורק אם
אם ורק אם 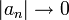
- בפרט
- תהי
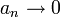 ותהי
ותהי 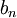 חסומה, אזי
חסומה, אזי 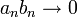
- תהיינה
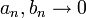 אזי גם
אזי גם 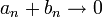
משפטי סנדביץ'
- משפט הסנדביץ' -
- תהיינה סדרות המקיימות לכל n כי
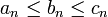
- כמו כן, יהי
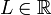 כך ש
כך ש 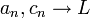
- אזי
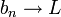
- תהיינה סדרות המקיימות לכל n כי
- חצי סנדביץ'-
- תהיינה סדרות המקיימות לכל n כי
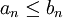
- כמו כן נתון כי
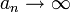
- אזי
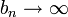
- תהיינה סדרות המקיימות לכל n כי
- חצי סנדביץ' על הרצפה -
- תהיינה סדרות המקיימות לכל n כי
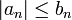
- כמו כן נתון כי
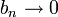
- אזי
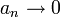
- תהיינה סדרות המקיימות לכל n כי
מבוא לחשבון גבולות (אריתמטיקה של גבולות)
- תהיינה
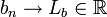 ,
, 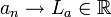 אזי
אזי
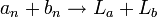
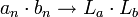
- אם
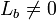 אזי
אזי 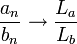
אינדוקציה
- משפט האינדוקציה המתמטית
- תהי סדרת טענות כך שמתקיימים שני התנאים הבאים:
- הטענה הראשונה נכונה.
- לכל
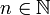 אם הטענה הn מתקיימת אז גם הטענה הn+1 מתקיימת.
אם הטענה הn מתקיימת אז גם הטענה הn+1 מתקיימת.
- אזי כל הטענות בסדרה נכונות
- אי שיוויון ברנולי: יהי
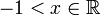 אזי לכל
אזי לכל 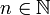 מתקיים כי
מתקיים כי 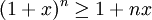
חזקת אינסוף
- תהי
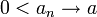 אזי:
אזי:
- אם
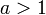 מתקיים כי
מתקיים כי 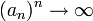
- אם
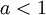 מתקיים כי
מתקיים כי 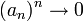
- אם
- שימו לב כי ייתכן ו
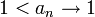 , כלומר איברי הסדרה גדולים מ1 אך גבולה הוא 1 ואז המשפט אינו תקף.
, כלומר איברי הסדרה גדולים מ1 אך גבולה הוא 1 ואז המשפט אינו תקף.
כלל המנה
- כלל המנה (הוכחה בסיכום הבא על אי-שוויון הממוצעים).
- תהי סדרה
 המקיימת כי גבול המנה הוא
המקיימת כי גבול המנה הוא 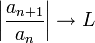 אזי:
אזי:
- אם
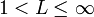 מתקיים כי
מתקיים כי 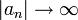
- אם
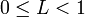 מתקיים כי
מתקיים כי 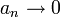
- מתקיים כי
![\sqrt[n]{|a_n|}\to L](/images/math/4/f/9/4f93143387173dbbb71b910524a94f06.png)
- אם
- תהי סדרה
- דוגמאות:
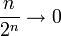
![\sqrt[n]{n}\to 1](/images/math/0/2/b/02be880c16c342f3ede5bc48390ba476.png)
- עבור
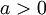 מתקיים
מתקיים ![\sqrt[n]{a}\to 1](/images/math/4/d/d/4dd173cb328b88deee1819cb97cc415d.png)
![\sqrt[n]{n!}\to \infty](/images/math/7/1/1/711dfc826d7a0c8a163182313e2b6535.png)
חזקות של גבולות
- יהי
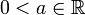 ותהי
ותהי 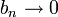 אזי
אזי 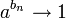
- רעיון הוכחה: אם
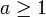 אזי
אזי 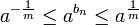 והרי
והרי ![\sqrt[m]{a}\to 1](/images/math/b/7/4/b74ed88b145e95e30a6783066a8d4f3f.png) לפי כלל המנה
לפי כלל המנה
- רעיון הוכחה: אם
- יהי
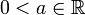 ותהי
ותהי 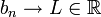 אזי
אזי 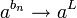
- רעיון הוכחה:
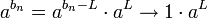
- רעיון הוכחה:
- תהי
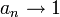 ותהי
ותהי 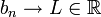 אזי
אזי 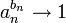
- רעיון הוכחה:
![a_n^{[L]-1}\leq a_n^{b_n}\leq a_n^{[L]+1}](/images/math/d/a/8/da8de49160634c7a0cea134d3d2862b3.png) לפי חשבון גבולות (כפל) שני הצדדים שואפים ל1. (אם
לפי חשבון גבולות (כפל) שני הצדדים שואפים ל1. (אם 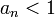 אי השיוויון הפוך).
אי השיוויון הפוך).
- רעיון הוכחה:
- תהי
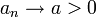 ותהי
ותהי 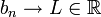 אזי
אזי 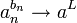
- רעיון הוכחה:
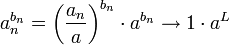
- רעיון הוכחה:
- תהי
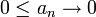 ותהי
ותהי 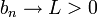 אזי
אזי 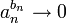
- רעיון הוכחה: החל משלב מסויים
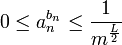
- רעיון הוכחה: החל משלב מסויים
סדרות מונוטוניות והמספר e
- כל סדרה מונוטונית הינה חסומה מתכנסת לגבול סופי, או שאינה חסומה ושואפת לגבול אינסופי.
- דוגמא: נביט בסדרה
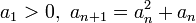
- כיוון ש
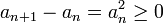 מדובר בסדרה מונוטונית עולה.
מדובר בסדרה מונוטונית עולה. - אם הסדרה חסומה:
- קיים לה גבול סופי
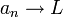
- נחשב את גבול שני צידי המשוואה
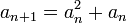
- לכן
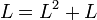 ולכן
ולכן 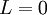
- אבל הסדרה עולה וחסומה מלמטה ע"י האיבר הראשון ולכן
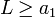
- כלומר
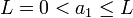 בסתירה.
בסתירה.
- קיים לה גבול סופי
- מכאן הסדרה אינה חסומה, וכיוון שהיא עולה
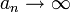
- כיוון ש
- המספר e (הוכחות בעזרת אי-שוויון הממוצעים).
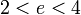 .
.
תתי סדרות וגבולות חלקיים
הגדרת גבול חלקי
- לכל סדרת מקומות
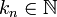 המקיימת לכל
המקיימת לכל  כי
כי 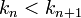 נגדיר כי
נגדיר כי 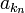 הינה תת סדרה של הסדרה
הינה תת סדרה של הסדרה 
- שימו לב כי מקומות תת הסדרה הם באותו הסדר כמו בסדרה המקורית, ואסור לחזור על איבר פעמיים.
- לדוגמא:
- נביט בסדרה
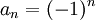
- אזי
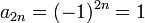 היא תת הסדרה של האיברים במקומות הזוגיים
היא תת הסדרה של האיברים במקומות הזוגיים 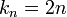
- נביט בסדרה
- נגדיר ש
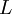 הוא גבול חלקי של הסדרה
הוא גבול חלקי של הסדרה  אם קיימת תת סדרה
אם קיימת תת סדרה 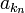 כך ש
כך ש 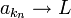
- טענה - יהי
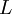 סופי או אינסופי, אזי:
סופי או אינסופי, אזי:
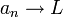 אם ורק אם לכל תת סדרה
אם ורק אם לכל תת סדרה 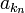 מתקיים כי
מתקיים כי 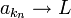
משפט בולצאנו-ויירשטראס
- לכל סדרה יש תת סדרה מונוטונית.
- משפט בולצאנו-ויירשטראס - לכל סדרה חסומה יש תת סדרה מתכנסת.
גבול עליון וגבול תחתון
- תהי סדרה

- נגדיר את הגבול העליון שלה (limsup):
- אם
 אינה חסומה מלעיל אזי
אינה חסומה מלעיל אזי 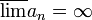
- אם
 חסומה מלעיל ויש לה גבול חלקי סופי כלשהו, נגדיר את
חסומה מלעיל ויש לה גבול חלקי סופי כלשהו, נגדיר את 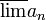 להיות החסם העליון של קבוצת הגבולות החלקיים של הסדרה
להיות החסם העליון של קבוצת הגבולות החלקיים של הסדרה - אחרת, נגדיר
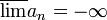
- אם
- נגדיר את הגבול התחתון שלה (liminf):
- אם
 אינה חסומה מלרע אזי
אינה חסומה מלרע אזי 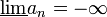
- אם
 חסומה מלרע ויש לה גבול חלקי סופי כלשהו, נגדיר את
חסומה מלרע ויש לה גבול חלקי סופי כלשהו, נגדיר את 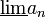 להיות החסם התחתון של קבוצת הגבולות החלקיים של הסדרה
להיות החסם התחתון של קבוצת הגבולות החלקיים של הסדרה - אחרת, נגדיר
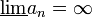
- אם
- לכל גבול חלקי L של הסדרה מתקיים כי:
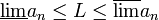
- הגבול העליון והגבול התחתון הם גבולות חלקיים (כלומר יש תת סדרה ששואפת לגבול העליון, ויש תת סדרה ששואפת לגבול התחתון).
- לכל
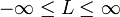 מתקיים כי
מתקיים כי 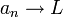 אם ורק אם
אם ורק אם 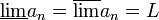
תתי סדרות המכסות סדרה
- אם ניתן לחלק סדרה למספר סופי של תתי סדרות המכסות את כולה, וכולן שואפות לאותו הגבול - אזי הסדרה כולה שואפת לגבול זה.
- ייתכן שניתן לחלק סדרה לאינסוף תתי סדרות שכולם שואפות לאותו הגבול, אך הסדרה לא תשאף לגבול זה.
כלל הe
- תהי
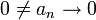 אזי
אזי 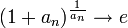
- אם
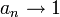 אזי
אזי 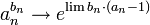
![a_n^{b_n}=\left[\left(1+(a_n-1)\right)^{\frac{1}{a_n-1}}\right]^{ b_n\cdot (a_n-1)}](/images/math/1/b/e/1be3fddf2ca563da0e4e631530a64ce5.png) .
.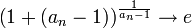 בין אם
בין אם 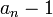 שלילי או חיובי, לפי הטענות לעיל.
שלילי או חיובי, לפי הטענות לעיל.- שימו לב שאם
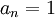 , אז ממילא מקבלים 1 בנוסחא הסופית, ואז לא צריך לחלק ב
, אז ממילא מקבלים 1 בנוסחא הסופית, ואז לא צריך לחלק ב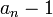 ששווה אפס.
ששווה אפס.
- דוגמא:
חשבון גבולות (אריתמטיקה של גבולות)
- אריתמטיקה מורחבת (הכתיב הוא מקוצר ואינו מדוייק):
- חסומה כפול אפיסה = אפיסה
- חסומה חלקי אינסוף = אפיסה
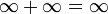
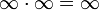
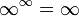
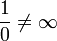
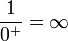
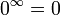
- אינסוף כפול סדרה השואפת למספר חיובי = אינסוף.
- יש גבול סופי + אין גבול סופי = אין גבול סופי.
- אינסוף ועוד חסומה שווה אינסוף.
- אינסוף בחזקת מספר חיובי זה אינסוף
- סדרה השואפת לגבול גדול מאחד, בחזקת אינסוף זה אינסוף.
- סדרה השואפת לגבול בין מינוס אחד לאחד לא כולל, בחזקת אינסוף, זה אפס.
המקרים הבעייתיים
- המקרים הבעייתיים בהם צריך להפעיל מניפולציות אלגבריות או משפטים על מנת לחשב את הגבול:
קריטריון קושי לסדרות
- דוגמא: הסדרה
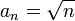 מקיימת כי
מקיימת כי 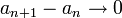 אך היא אינה מתכנסת למספר סופי אלא שואפת לאינסוף.
אך היא אינה מתכנסת למספר סופי אלא שואפת לאינסוף.
- הגדרה: סדרה
 מקיימת את קריטריון קושי (ונקראת סדרת קושי) אם:
מקיימת את קריטריון קושי (ונקראת סדרת קושי) אם: - לכל מרחק
 קיים מקום
קיים מקום 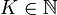 כך שאחריו לכל זוג מקומות
כך שאחריו לכל זוג מקומות 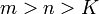 מתקיים כי
מתקיים כי 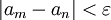 (המרחק בין האיברים במקומות הללו קטן מאפסילון).
(המרחק בין האיברים במקומות הללו קטן מאפסילון).
- משפט: בממשיים, סדרה מתכנסת לגבול סופי אם ורק אם היא סדרת קושי.
- תרגיל: תהי סדרה המקיימת לכל n כי
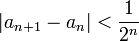 אזי היא מתכנסת למספר סופי.
אזי היא מתכנסת למספר סופי.
פרק 3 - טורים
מבוא והגדרה
- תהי סדרה
 , נגדיר את סדרת הסכומים החלקיים (סס"ח בקיצור) של
, נגדיר את סדרת הסכומים החלקיים (סס"ח בקיצור) של  ע"י
ע"י
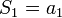
- ולכל
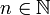 מתקיים
מתקיים 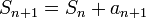
- במילים אחרות,
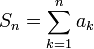
- הגדרת הטור
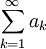
- אומרים כי
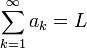 אם
אם 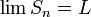
- אומרים כי
- אם לסס"ח יש גבול סופי אומרים כי הטור מתכנס, ואילו אם אין לה גבול סופי אומרים כי הטור מתבדר.
- שימו לב כי בעצם:
- אם הטור
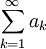 מתכנס, אזי
מתכנס, אזי 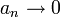
- הוכחה:
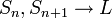
- לכן
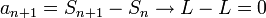
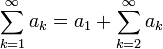
- מסקנה: שינוי מספר סופי של איברי הטור לא משפיע על התכנסות, אבל כן משפיע על סכום הטור.
חשבון טורים
- אם הטור
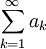 מתכנס, ו
מתכנס, ו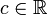 קבוע אזי
קבוע אזי
- אם הטורים
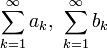 מתכנסים אזי
מתכנסים אזי
הטור ההנדסי
- הטור
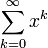 מתכנס אם ורק אם
מתכנס אם ורק אם 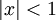 וכאשר הוא מתכנס מתקיים כי:
וכאשר הוא מתכנס מתקיים כי:
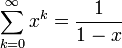 וכמו כן
וכמו כן 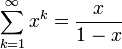
טור מקל סלפי (טלסקופי)
- חישוב
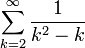 על ידי הסס"ח הטלסקופי
על ידי הסס"ח הטלסקופי
- חישוב
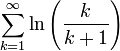 על ידי הסס"ח הטלסקופי
על ידי הסס"ח הטלסקופי
העשרה על סוגי סכימה
התכנסות בהחלט
- משפט: אם טור הערכים המוחלטים
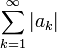 מתכנס, אזי גם הטור המקורי
מתכנס, אזי גם הטור המקורי 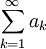 מתכנס.
מתכנס.
- הגדרה:
- הטור
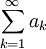 נקרא מתכנס בהחלט אם
נקרא מתכנס בהחלט אם 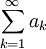 מתכנס וגם
מתכנס וגם 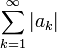 מתכנס
מתכנס - הטור
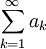 נקרא מתכנס בתנאי אם
נקרא מתכנס בתנאי אם 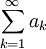 מתכנס אך
מתכנס אך 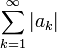 מתבדר
מתבדר - הטור
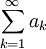 נקרא מתבדר אם
נקרא מתבדר אם 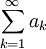 מתבדר וגם
מתבדר וגם 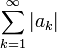 מתבדר
מתבדר
- הטור
- משפט: (הכללת אי שיוויון המשולש) יהי טור מתכנס בהחלט, אזי:
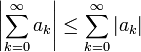
- הוכחה:
- לפי אי שיוויון המשולש, לכל n סופי מתקיים כי
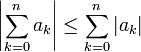
- ולכן גם הגבול של הסדרה השמאלית קטן או שווה לגבול של הסדרה הימנית, וזו התוצאה שרצינו.
מבחני התכנסות לטורים חיוביים
הקדמה והטור ההרמוני
- הגדרה: טור
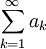 נקרא טור חיובי אם לכל n מתקיים כי
נקרא טור חיובי אם לכל n מתקיים כי 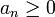 .
. - סדרת הסכומים החלקיים של טור חיובי היא מונוטונית עולה, לכן הטור מתכנס אם ורק אם היא חסומה.
- לסס"ח של הטור ההרמוני
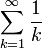 יש תת סדרה ששואפת לאינסוף, ולכן הטור מתבדר:
יש תת סדרה ששואפת לאינסוף, ולכן הטור מתבדר:
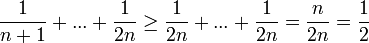
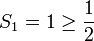
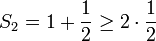
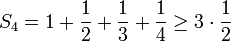
- ...
- באופן כללי
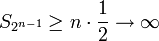
מבחני ההשוואה
- מבחן ההשוואה הראשון-
- תהיינה סדרות כך ש
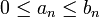 לכל n. אזי:
לכל n. אזי:
- אם הטור הגדול יותר
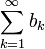 מתכנס בוודאי הטור הקטן יותר
מתכנס בוודאי הטור הקטן יותר 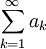 מתכנס.
מתכנס. - נובע מכך לוגית שאם הטור הקטן מתבדר, הטור הגדול מתבדר.
- אם הטור הגדול יותר
- דוגמא:
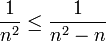
- ראינו שהטור החיובי
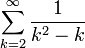 מתכנס ולכן לפי מבחן ההשוואה הראשון גם הטור החיובי
מתכנס ולכן לפי מבחן ההשוואה הראשון גם הטור החיובי 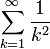 מתכנס
מתכנס
- מבחן ההשוואה הגבולי-
- תהיינה סדרות
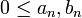 כך ש
כך ש 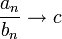 אזי:
אזי:
- אם
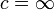 אזי
אזי 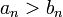 החל משלב מסויים, ולכן אם
החל משלב מסויים, ולכן אם 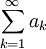 מתכנס גם
מתכנס גם 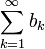 מתכנס
מתכנס - אם
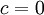 אזי
אזי 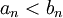 החל משלב מסויים, ולכן אם
החל משלב מסויים, ולכן אם 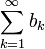 מתכנס גם
מתכנס גם 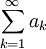 מתכנס
מתכנס - אחרת,
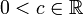 והטורים חברים
והטורים חברים 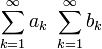 , כלומר
, כלומר 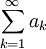 מתכנס אם ורק אם
מתכנס אם ורק אם 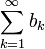 מתכנס
מתכנס
- אם
- דוגמא:
מבחני השורש והמנה
- יהי טור
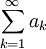
- מבחן המנה -
- אם
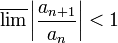 אזי הטור מתכנס בהחלט
אזי הטור מתכנס בהחלט - אם
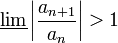 אזי
אזי 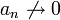 ולכן הטור מתבדר
ולכן הטור מתבדר
- אם
- מבחן השורש -
- אם
![\overline{\lim}\sqrt[n]{|a_n|}<1](/images/math/1/7/0/170a41ea6dd2d7144f4ddcddb3fdd0fc.png) אזי הטור מתכנס בהחלט
אזי הטור מתכנס בהחלט - אם
![\overline{\lim}\sqrt[n]{|a_n|}>1](/images/math/d/8/7/d8720dc79fa493970dfb27d4014802c5.png) אזי
אזי 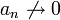 ולכן הטור מתבדר
ולכן הטור מתבדר
- אם
- שימו לב - במבחן השורש לוקחים את הגבול העליון בשני המקרים, ובמבחן המנה צריך שהעליון יהיה קטן מאחד, או התחתון גדול מאחד. זו לא טעות...
מבחן העיבוי
- מבחן העיבוי-
- תהי
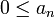 סדרה מונוטונית יורדת אזי הטור
סדרה מונוטונית יורדת אזי הטור 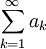 מתכנס אם ורק אם
מתכנס אם ורק אם 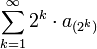 מתכנס
מתכנס
- תהי
- הוכחה:
- ראשית, נוכיח באינדוקציה כי
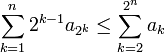 כלומר
כלומר 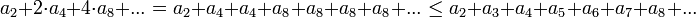
- כעת נוכיח באינדוקציה כי
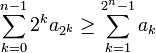
- ראשית, נוכיח באינדוקציה כי
- סה"כ אם הטור האחד מתכנס, הסס"ח של השני חסומה ולכן גם השני מתכנס.
הטור ההרמוני המוכלל
- הטור
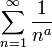 מתכנס אם ורק אם
מתכנס אם ורק אם 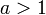
- דוגמאות:
מבחני התכנסות לטורים כלליים
מבחן דיריכלה
- תהי סדרה
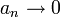 סדרה מונוטונית יורדת לאפס
סדרה מונוטונית יורדת לאפס - תהי סדרה
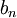 כך שההסס"ח שלה חסומה, כלומר קיים
כך שההסס"ח שלה חסומה, כלומר קיים 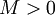 כך שלכל n מתקיים
כך שלכל n מתקיים 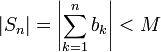
- אזי הטור
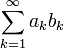 מתכנס.
מתכנס.
- הוכחה:
- נסמן ב
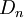 את סדרת הסכומים החלקיים של הטור
את סדרת הסכומים החלקיים של הטור 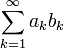 וב
וב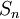 את סדרת הסכומים החלקיים של
את סדרת הסכומים החלקיים של 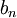 .
. - יהיו
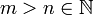
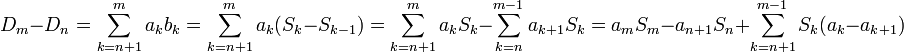
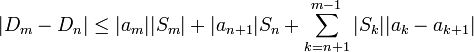
- כעת נשתמש בעובדה כי
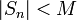 לכל n וכן
לכל n וכן 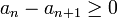 לכל n.
לכל n. 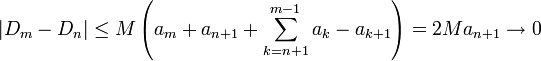
- לכן
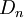 סדרת קושי ולכן מתכנסת לגבול סופי, כלומר הטור מתכנס.
סדרת קושי ולכן מתכנסת לגבול סופי, כלומר הטור מתכנס.
מבחן לייבניץ
- תהי
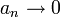 סדרה מונוטונית יורדת לאפס. אזי:
סדרה מונוטונית יורדת לאפס. אזי:
- הטור
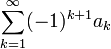 מתכנס.
מתכנס. 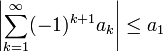 .
.
- הטור
- הוכחה:
- כיוןן שהסס"ח של
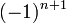 חסומה הטור מתכנס לפי מבחן דיריכלה.
חסומה הטור מתכנס לפי מבחן דיריכלה. - נסמן ב
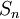 את הסס"ח של הטור
את הסס"ח של הטור 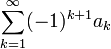 .
. - כיוון שהסדרה
 יורדת, ניתן להוכיח באינדוקציה כי:
יורדת, ניתן להוכיח באינדוקציה כי:
- כיוןן שהסס"ח של
סיכום בדיקת התכנסות 🖖
- כיצד נבחן אם הטור
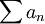 מתכנס בהחלט, בתנאי או מתבדר?
מתכנס בהחלט, בתנאי או מתבדר?
- אם ניתן להראות כי
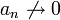 הטור מתבדר
הטור מתבדר - נבצע מבחני ספוק 🖖
- אם לפי מבחני ההשוואה (הראשון או הגבולי) הטור
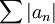 אינו מתכנס, אז אין התכנסות בהחלט, נעבר לבדוק התכנסות בתנאי.
אינו מתכנס, אז אין התכנסות בהחלט, נעבר לבדוק התכנסות בתנאי. - אם במבחן המנה או השורש הגבול גדול מ1 הטור מתבדר, אם קטן מ1 הטור מתכנס בהחלט ואם שווה ל1 צריך לנסות משהו אחר.
- אם במבחן העיבוי הטור
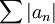 אינו מתכנס, אז אין התכנסות בהחלט, נעבר לבדוק התכנסות בתנאי.
אינו מתכנס, אז אין התכנסות בהחלט, נעבר לבדוק התכנסות בתנאי.
- אם לפי מבחני ההשוואה (הראשון או הגבולי) הטור
- אם לא מצאנו התכנסות בהחלט, נבצע מבחנים על טורים כלליים בשביל לבדוק התכנסות בתנאי
- מבחן לייבניץ
- מבחן דיריכלה
- עבודה ישירה על סדרת הסכומים החלקיים (טור טלסקופי למשל)
סכום האיברים החיוביים, וסכום האיברים השליליים
- תהי סדרה
 ונגדיר את:
ונגדיר את:
- הטור
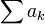 מתכנס בהחלט אם ורק אם הטורים
מתכנס בהחלט אם ורק אם הטורים 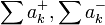 מתכנסים שניהם.
מתכנסים שניהם. - אם הטור
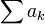 מתכנס בתנאי אזי הטורים
מתכנס בתנאי אזי הטורים 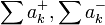 מתבדרים שניהם ושואפים לאינסוף.
מתבדרים שניהם ושואפים לאינסוף.
- כפי שהוכחנו בעבר בדרך שונה, אם הטור מתכנס בהחלט נובע ש
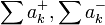 מתכנסים שניהם, וביחד עם העובדה ש
מתכנסים שניהם, וביחד עם העובדה ש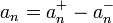 נובע שהטור מתכנס.
נובע שהטור מתכנס.
שינוי סדר הסכימה
- תהי
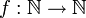 פונקציה הפיכה ותהי סדרה
פונקציה הפיכה ותהי סדרה  אז נאמר ש
אז נאמר ש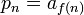 היא שינוי סדר של הסדרה
היא שינוי סדר של הסדרה  .
.
- תרגיל - אם
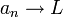 גם שינוי הסדר מקיים
גם שינוי הסדר מקיים 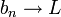
- דוגמא:
- בדוגמא האחרונה:
- נסמן ב
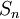 את הסס"ח של
את הסס"ח של  ומתקיים כי:
ומתקיים כי:
- נסמן ב
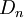 את הסס"ח של שינוי הסדר
את הסס"ח של שינוי הסדר 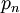 , מתקיים כי:
, מתקיים כי:
- שינוי הסדר אמנם הותיר את הטור מתבדר, אך הפך את סדרת הסכומים החלקיים מחסומה לשואפת לאינסוף.
משפט רימן
- משפט רימן - יהי טור מתכנס בתנאי
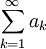 אזי לכל
אזי לכל 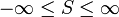 קיים שינוי סדר כך ש
קיים שינוי סדר כך ש 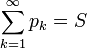
- כלומר, אם הטור מתכנס בתנאי, ניתן לגרום לו להתכנס לכל ערך שנרצה (ואף לשאוף לפלוס או מינוס אינסוף), על ידי שינוי סדר איברי הסדרה.
שינוי סדר הסכימה של טור מתכנס בהחלט
- יהי טור מתכנס בהחלט
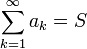 אזי לכל שינוי סדר
אזי לכל שינוי סדר 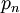 מתקיים כי
מתקיים כי 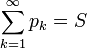
- כלומר, שינוי סדר איברי הסדרה אינו משפיע על סכום הטור.
פרק 4 - פונקציות ורציפות
מבוא לגבולות
- מבוא לגבולות (שיטות אלגבריות: כפל בצמוד, הוצאת חזקה משמעותית).
הגדרת הגבול לפי קושי
-
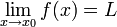 אם לכל סביבה של L בציר y קיימת סביבה של
אם לכל סביבה של L בציר y קיימת סביבה של  בציר x, כך שלכל ערכי x בסביבה של
בציר x, כך שלכל ערכי x בסביבה של  פרט אולי ל
פרט אולי ל עצמו, ערכי ציר y כלומר
עצמו, ערכי ציר y כלומר  נמצאים בסביבה של L בציר y.
נמצאים בסביבה של L בציר y.
- דוגמאות:
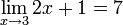 אם לכל
אם לכל  קיים
קיים 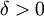 כך שלכל x המקיים
כך שלכל x המקיים 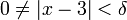 מתקיים
מתקיים 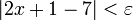
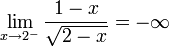 אם לכל
אם לכל 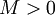 קיים
קיים 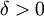 כך שלכל x המקיים
כך שלכל x המקיים 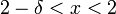 מתקיים כי
מתקיים כי 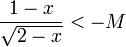
 אסימפטוטה אופקית מימין של
אסימפטוטה אופקית מימין של  אם לכל
אם לכל  קיים
קיים 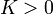 כך שלכל x המקיים
כך שלכל x המקיים 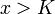 מתקיים כי
מתקיים כי 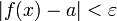
הגדרת הגבול לפי היינה
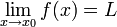 אם לכל סדרת מספרים על ציר איקס
אם לכל סדרת מספרים על ציר איקס 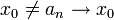 סדרת המספרים על ציר y מקיימת
סדרת המספרים על ציר y מקיימת 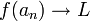
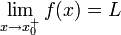 אם לכל סדרת מספרים על ציר איקס
אם לכל סדרת מספרים על ציר איקס 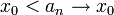 סדרת המספרים על ציר y מקיימת
סדרת המספרים על ציר y מקיימת 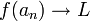
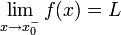 אם לכל סדרת מספרים על ציר איקס
אם לכל סדרת מספרים על ציר איקס 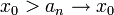 סדרת המספרים על ציר y מקיימת
סדרת המספרים על ציר y מקיימת 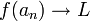
הגדרה זו שקולה להגדרה של קושי, כלומר הגבול שווה לL לפי קושי אם ורק אם הוא שווה לL לפי היינה.
- מרבית כללי האריתמטיקה המורחבות נובעים "בחינם" עבור פונקציות
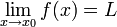 אם ורק אם
אם ורק אם 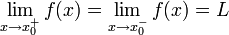
הפונקציות הטריגונומטריות
- הגדרת סינוס וקוסינוס ע"י מעגל היחידה.
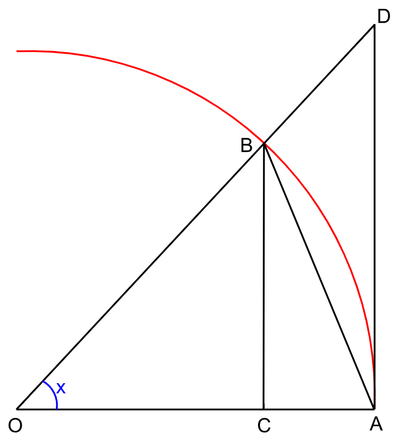
- עבור זוית
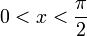 שטח המשולש חסום בשטח הגזרה (משולש פיצה עם הקשה) שחסום בשטח המשולש:
שטח המשולש חסום בשטח הגזרה (משולש פיצה עם הקשה) שחסום בשטח המשולש: 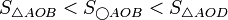
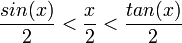
- כיוון ש
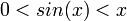 בתחום
בתחום 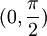 , נובע לפי סנדוויץ' ש
, נובע לפי סנדוויץ' ש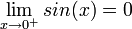 .
. - כיוון שמדובר בפונקציה אי זוגית, נובע שזה גם הגבול משני הצדדים.
- כעת בתחום
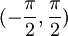 הקוסינוס חיובית ולכן
הקוסינוס חיובית ולכן 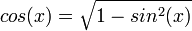 ונובע כי
ונובע כי 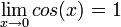 .
.
- כיוון ש
- נחלק את אי השיוויון הטריגונומטרי בסינוס ונקבל:
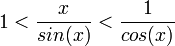
- לפי כלל הסנדביץ
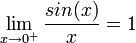
- כיוון שמדובר בפונקציה זוגית, נובע שהגבול משני הצדדים שווה 1.
- עבור זוית
- ראינו ש
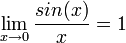 .
. - שימו לב ש
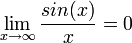 , כיוון שמדובר בחסומה חלקי שואפת לאינסוף.
, כיוון שמדובר בחסומה חלקי שואפת לאינסוף.
רציפות
- רציפות.
- הגדרה:
- פונקציה f נקראית רציפה בקטע
![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) אם f רציפה בכל נקודה בקטע
אם f רציפה בכל נקודה בקטע 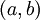 ובנוסף
ובנוסף 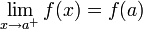 וגם
וגם 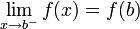
- טענה: אם f רציפה ב
 אזי לכל סדרה
אזי לכל סדרה  (גם אם אינה שונה מ
(גם אם אינה שונה מ ) מתקיים כי
) מתקיים כי 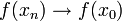 .
.
- גבול של הרכבת פונקציות נכשל ללא רציפות.
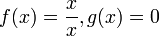 מתקיים כי
מתקיים כי 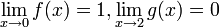 אבל
אבל 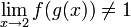 .
.
- הרכבת רציפות: תהי f רציפה ב
 ותהי g רציפה ב
ותהי g רציפה ב . אזי
. אזי 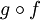 רציפה ב
רציפה ב .
.
- הוכחה:
- תהי סדרה
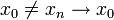 אזי
אזי 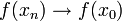
- לפי הטענה הקודמת,
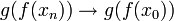 .
.
- פונקציות הפיכות (הוכחות והגדרות מדוייקות בבדידה).
- פונקציה
![f:[a,b]\to [c,d]](/images/math/6/a/d/6ad907c775ff05b8176b946ff921b21c.png) הפיכה אם"ם היא חח"ע ועל
הפיכה אם"ם היא חח"ע ועל - הפונקציה ההופכית היא
![f^{-1}:[c,d]\to[a,b]](/images/math/a/0/3/a03dbad0cc5ab3eebe2bba1a2c7bd947.png) ומתקיים כי
ומתקיים כי 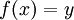 אם"ם
אם"ם 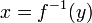
- פונקציה
- טענה: אם
![f:[a,b]\to [c,d]](/images/math/6/a/d/6ad907c775ff05b8176b946ff921b21c.png) רציפה בקטע
רציפה בקטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) , אזי
, אזי ![f^{-1}:[c,d]\to[a,b]](/images/math/a/0/3/a03dbad0cc5ab3eebe2bba1a2c7bd947.png) רציפה בקטע
רציפה בקטע ![[c,d]](/images/math/c/3/1/c31d2b7df15fa7d119c2f8d13f69e10b.png) .
.
- הוכחה:
- תהי
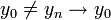 , צ"ל ש
, צ"ל ש 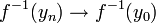
- יהי גבול חלקי
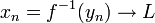 .
. - אזי
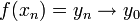 .
. - מצד שני, לפי רציפות הפונקציה f מתקיים
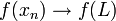 .
. - לכן
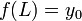 ולכן
ולכן 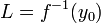 .
.
אי רציפות
- מיון אי רציפות.
- רציפות - הגבול בנקודה שווה לערך בנקודה.
- סליקה - הגבול קיים וסופי בנקודה, אך שונה מהערך בנקודה או שהפונקציה אינה מוגדרת בנקודה.
- קפיצתית (מין ראשון) - הגבולות החד צדדיים קיימים סופיים ושונים בנקודה.
- עיקרית (מין שני) - אחד הגבולות החד צדדיים אינו קיים או שאינו סופי.
פרק 5 - גזירות
הגדרת הנגזרת
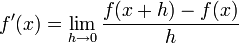
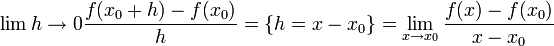
- הסבר לגבי שיטת ההצבה בה השתמשנו לעיל:
- נניח כי
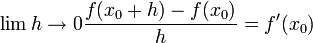 ונוכיח כי
ונוכיח כי 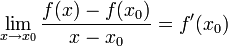 , והוכחה דומה בכיוון ההפוך.
, והוכחה דומה בכיוון ההפוך. - תהי
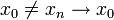 נגדיר את הסדרה
נגדיר את הסדרה 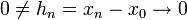 .
. - כיוון ש
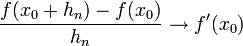 נובע כי
נובע כי 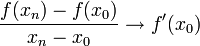 .
.
- אם f גזירה בנקודה, היא רציפה בנקודה:
- צ"ל
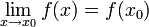
- לפי אריתמטיקה של גבולות זה שקול ל
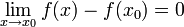
- לפי עקרון win (קיצור של wouldn't it be nice?) מתקיים כי
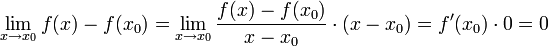
- צ"ל
- פונקציה הערך המוחלט אינה גזירה באפס
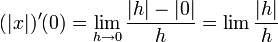 וגבול זה אינו קיים, כיוון שהגבולות החד צדדים שונים.
וגבול זה אינו קיים, כיוון שהגבולות החד צדדים שונים.- ניתן לשים לב גם ש
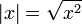 , וכמו כן נראה בהמשך כי
, וכמו כן נראה בהמשך כי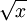 אינה גזירה באפס.
אינה גזירה באפס.
הנגזרות של הפונקציות האלמנטריות
- טריגו:
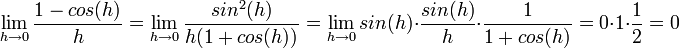
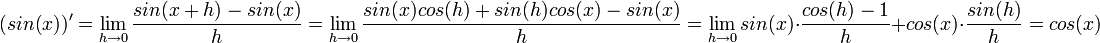
- באופן דומה
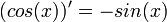
- לוג:
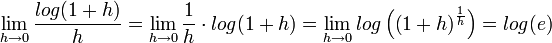
- המעבר האחרון נובע מהעובדה שפונקצית הלוג רציפה.
- (בפרט נובע כי
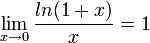 .)
.)
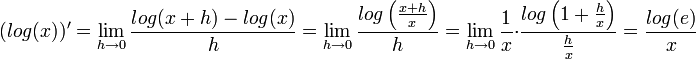
- בפרט נובע כי
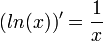
- בפרט נובע כי
- אקספוננט:
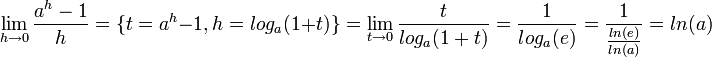
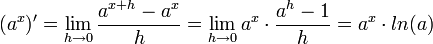
- בפרט נובע כי
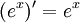 .
.
- בפרט נובע כי
- ישר:
חוקי הגזירה
- תהיינה f,g גזירות ב
 אזי:
אזי:
תהי g גזירה ב ותהי f הגזירה ב
ותהי f הגזירה ב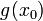 :
:
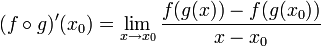
- תהי סדרה
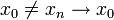 .
. - רוצים לומר ש
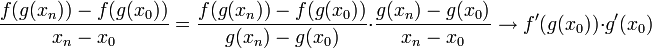 .
. - אמנם
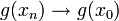 בגלל שהרציפות נובעת מהגזירות, אבל לא ידוע ש
בגלל שהרציפות נובעת מהגזירות, אבל לא ידוע ש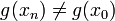 ובמקרה זה אנחנו כופלים ומחלקים באפס.
ובמקרה זה אנחנו כופלים ומחלקים באפס. - אם יש תת סדרה
 של
של 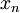 עבורה
עבורה 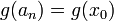 אזי
אזי 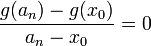 ולכן
ולכן 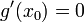 .
. - לכן
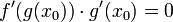 .
. - כמו כן,
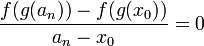 .
. - לכן בכל מקרה קיבלנו כי
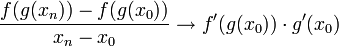
- סה"כ
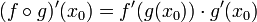 .
.
נגזרת של חזקה
- עבור
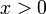 מתקיים
מתקיים 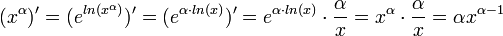
- עבור חזקות בהן הביטוי מוגדר,
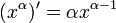 גם עבור
גם עבור 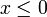 (לפי תכונות של פונקציות זוגיות ואי זוגיות, ובאפס לפי חישוב ישיר).
(לפי תכונות של פונקציות זוגיות ואי זוגיות, ובאפס לפי חישוב ישיר).
- חזקה:
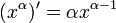 לכל
לכל 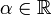 , הוכחה בהמשך.
, הוכחה בהמשך.
- בפרט:
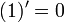
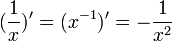
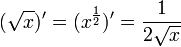
- עבור
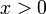 מתקיים
מתקיים ![(\sqrt[3]{x})'=(x^{\frac{1}{3}})'=\frac{1}{3\sqrt[3]{x^2}}](/images/math/5/3/d/53db7400bc58305de0bd6433f4af6db3.png) וכיוון שהפונקציה אי זוגית נובע שהנגזרת שווה לביטוי הזה גם לשאר ערכי x.
וכיוון שהפונקציה אי זוגית נובע שהנגזרת שווה לביטוי הזה גם לשאר ערכי x.
- דוגמא: חישוב הנגזרת של
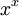
נגזרת מנה
תהיינה f,g גזירות בנקודה x כך ש 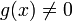 :
:
- נזכור כי
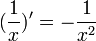
- אזי בנקודה x מתקיים:
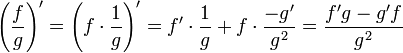
פונקציות הופכיות ונגזרתן
- טענה: תהי
![f:[a,b]\to [c,d]](/images/math/6/a/d/6ad907c775ff05b8176b946ff921b21c.png) הפיכה ורציפה. ונניח כי היא גזירה בנק'
הפיכה ורציפה. ונניח כי היא גזירה בנק' 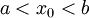 כך ש
כך ש 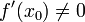 .
.
- אזי
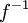 גזירה בנק'
גזירה בנק'  ומתקיים כי
ומתקיים כי 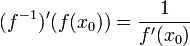 או בנוסח אחר-
או בנוסח אחר-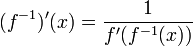
- הוכחה:
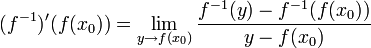
- תהי
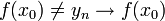 ונסמן
ונסמן 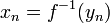 .
. - אזי מתוך רציפות וחח"ע נובע כי
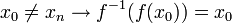
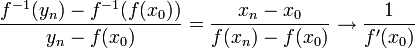
- דוגמא חשובה:
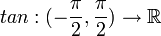 הפיכה וההופכית שלה נקראית
הפיכה וההופכית שלה נקראית 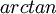 .
.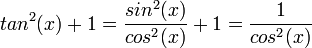
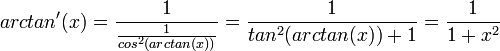
- הנגזרות של
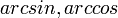
פרק 6 - חקירה
משפט ערך הביניים
- תהי f רציפה בקטע
![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) כאשר
כאשר 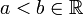 .
. - עוד נניח כי
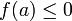 וכן
וכן 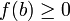 .
. - אזי קיימת נקודה
![c\in[a,b]](/images/math/0/0/a/00a49aece4cc72157b51ca282347a0f8.png) כך ש
כך ש 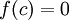
- תהי f רציפה ב
![[0,1]](/images/math/c/c/f/ccfcd347d0bf65dc77afe01a3306a96b.png) כך ש
כך ש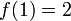 , הוכיחו שקיימת נק'
, הוכיחו שקיימת נק' ![c\in [0,1]](/images/math/6/e/a/6ea0a95f41192a6ad436a6874796e0cb.png) עבורה
עבורה 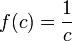
- נעביר אגף ונביט בפונקציה
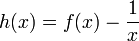 שצריך למצוא שורש שלה.
שצריך למצוא שורש שלה. 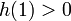 .
.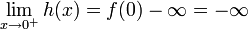 ולכן קיימת נקודה
ולכן קיימת נקודה 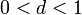 עבורה
עבורה 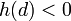 .
.- לפי משפט ערך הביניים בקטע
![[d,1]](/images/math/f/5/d/f5dbfa5a8804773df765ab6203ce1ae4.png) קיימת נק' המאפסת את הפונקציה h.
קיימת נק' המאפסת את הפונקציה h.
- נעביר אגף ונביט בפונקציה
משפטי ויירשטראס
- פונקציה רציפה בקטע סופי סגור - חסומה.
- פונקציה רציפה בקטע סופי סגור - מקבלת מינימום ומקסימום.
משפט פרמה
- אם פונקציה גזירה בנק' קיצון מקומי, הנגזרת שווה שם לאפס.
- ההפך אינו נכון, ייתכן שהנגזרת תתאפס אך בנקודה לא יהיה קיצון ואף לא פיתול.
משפט רול
- תהי f רציפה ב
![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) וגזירה ב
וגזירה ב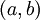 כך ש
כך ש 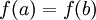 אזי קיימת נקודה
אזי קיימת נקודה 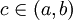 כך ש
כך ש 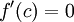
- תהי f רציפה ב
- כלומר, פונקציה רציפה בקטע סגור, וגזירה בקטע הפתוח, שמקבלת את אותו ערך בקצוות - הנגזרת שלה מתאפסת בנקודה כלשהי בקטע הפתוח.
- לפולינום מדרגה n יש לכל היותר n שורשים שונים.
משפט לגראנז' ותחומי עלייה וירידה
- פונקציה f נקראת עולה בתחום A אם לכל
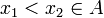 מתקיים כי
מתקיים כי 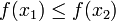
- פונקציה f נקראת יורדת בתחום A אם לכל
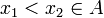 מתקיים כי
מתקיים כי 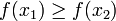
- תהי f רציפה ב
![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) וגזירה ב
וגזירה ב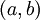 אזי קיימת נקודה
אזי קיימת נקודה 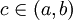 כך ש
כך ש 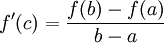
- כלומר קיימת נקודה בה השיפוע שווה לשיפוע המיתר בין שתי הנקודות בקצוות הקטע.
- תהי f רציפה ב
![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) וגזירה ב
וגזירה ב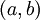 אזי f עולה בקטע
אזי f עולה בקטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) אם ורק אם
אם ורק אם 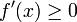 לכל
לכל ![x\in[a,b]](/images/math/8/2/9/8290bddba5acf9822dcbf61f4ac67d1b.png)
- כמו כן, באותם תנאים, אם
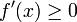 לכל
לכל ![x\in[a,b]](/images/math/8/2/9/8290bddba5acf9822dcbf61f4ac67d1b.png) אזי
אזי 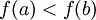 או שהפונקציה קבועה ב
או שהפונקציה קבועה ב![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) ונגזרתה שווה אפס בקטע
ונגזרתה שווה אפס בקטע 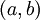
- דוגמא
- יהי
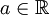 מצאו כמה פתרונות יש למשוואה
מצאו כמה פתרונות יש למשוואה 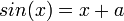
משפט קושי (לגראנז' המוכלל)
- תהיינה f,g רציפות ב
![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) וגזירות ב
וגזירות ב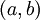 כך ש
כך ש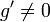 בקטע
בקטע 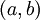 .
. - אזי קיימת נקודה
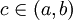 כך ש
כך ש 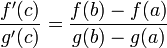
- הוכחת משפט לגראנז' המוכלל, שמוכיח גם את משפט לגראנז' עצמו כמקרה פרטי.
- ראשית, כיוון ש
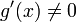 בקטע
בקטע 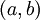 נובע לפי רול כי
נובע לפי רול כי 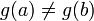 ולכן מותר לחלק בהפרש ביניהם.
ולכן מותר לחלק בהפרש ביניהם. 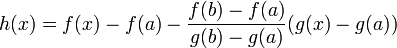
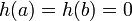 ולכן לפי רול קיימת נק'
ולכן לפי רול קיימת נק' 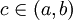 עבורה
עבורה 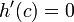 וזה מה שרצינו להוכיח.
וזה מה שרצינו להוכיח.- (שימו לב שמותר לחלק ב
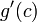 .)
.) - עבור
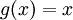 נקבל את משפט לאגראנז' הרגיל.
נקבל את משפט לאגראנז' הרגיל.
- ראשית, כיוון ש
כלל לופיטל
- תהיינה פונקציות כך ש
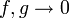 או
או 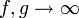 ונניח כי
ונניח כי 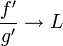 אזי גם
אזי גם 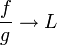
משפט סדרי הגודל
- לכל
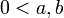 מתקיים כי:
מתקיים כי:
דוגמאות נוספות
הוכחת כלל לופיטל בשני המקרים
אהבתם חדו"א 1? אז תעופו על חדו"א 2!
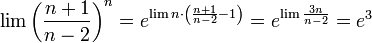
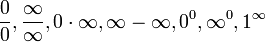
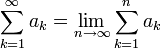
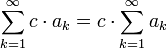
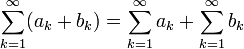
![\sum_{k=1}^\infty \frac{1}{\left(\sqrt[k]{k!}\right)^2} \sim \sum_{k=1}^\infty\frac{1}{k^2}](/images/math/c/a/e/cae290a62eae8711875fe2d047b719d4.png)
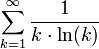
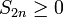
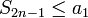
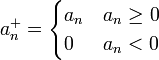
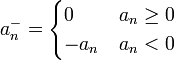
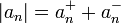
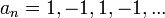
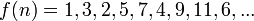
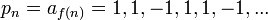
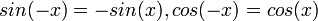
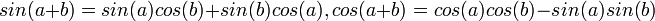
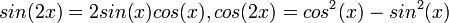
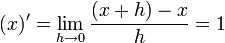
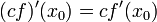
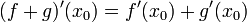
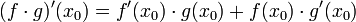
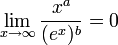
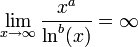
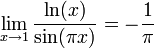
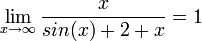
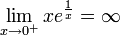
![\displaystyle{\lim_{x\to\infty} \sqrt[x]{x} =1}](/images/math/e/2/9/e290f0d53981cf203957134d534223de.png)